Fig_12

%図12.14
%
clear all; close all;

%1次遅れ系のパラメータを与える
T1 = 0.1; %時定数T=0.1の場合
T2 = 1.0; %時定数T=1の場合
T3 = 10.0; %時定数T=10の場合

%伝達関数の分子・分母多項式を与える
num = [ 0 1 ]; %分子多項式
den1 = [ T1 1 ]; %T=0.1の場合の分母多項式
den2 = [ T2 1 ]; %T=1の場合の分母多項式
den3 = [ T3 1 ]; %T=10の場合の分母多項式

%伝達関数表現を与える
sys1 = tf( num, den1 ); %T=0.1の場合の伝達関数表現
sys2 = tf( num, den2 ); %T=1の場合の伝達関数表現
sys3 = tf( num, den3 ); %T=10の場合の伝達関数表現

%角周波数の範囲を指定
w = logspace(-2, 2, 1000); %対数的に等間隔なベクトルの生成(10^{-2}から10^{2}で1000点)

%ゲインと位相の計算
[ gain1 phase1 w1 ] = bode( sys1, w ); %ゲインと位相
gain1 = gain1(:); %T=0.1の場合のゲインの配列を1次元ベクトルに変換
gain1dB = 20*log10(gain1); %T=0.1の場合のゲインをデシベル値に変換

[ gain2 phase2 w2 ] = bode( sys2, w ); %ゲインと位相
gain2 = gain2(:); %T=1の場合のゲインの配列を1次元ベクトルに変換
gain2dB = 20*log10(gain2); %T=1の場合のゲインをデシベル値に変換

[ gain3 phase3 w3 ] = bode( sys3, w ); %ゲインと位相
gain3 = gain3(:); %T=10の場合のゲインの配列を1次元ベクトルに変換
gain3dB = 20*log10(gain3); %T=10の場合のゲインをデシベル値に変換

%ゲイン線図のプロット
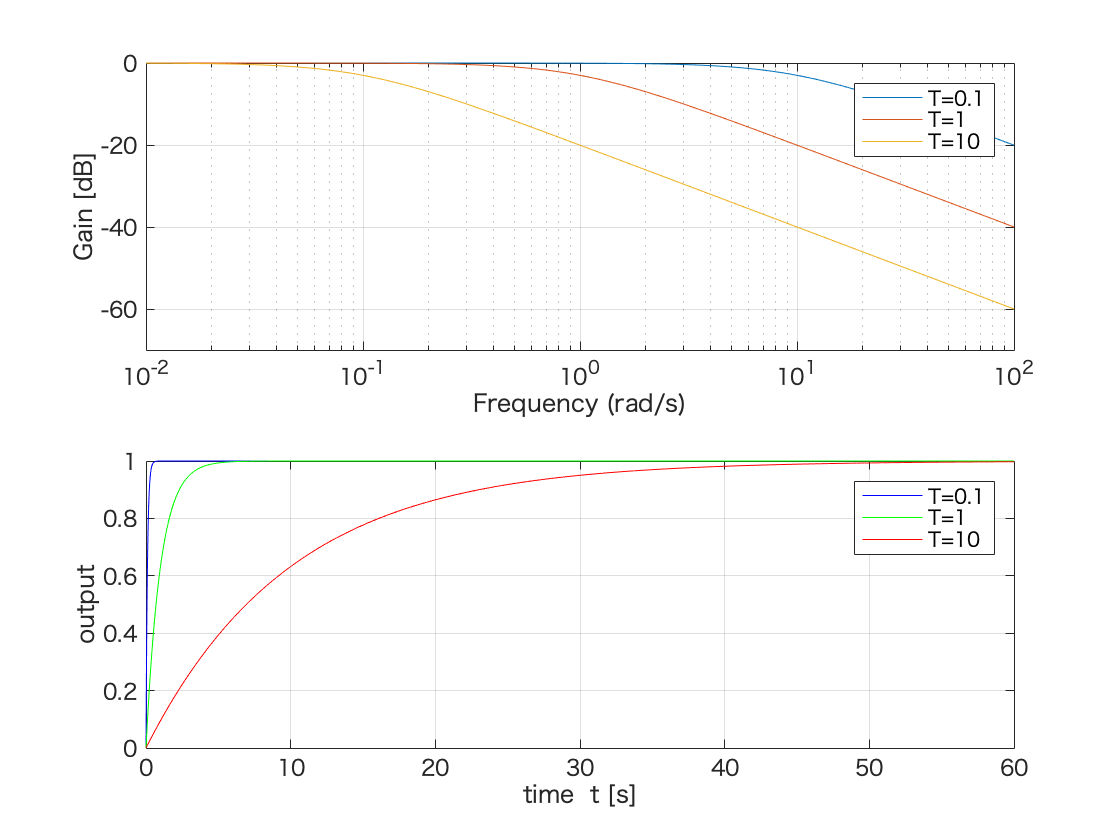
subplot(2,1,1) %複数の図を並べるためのコマンド．2行1列の1行目という意味
semilogx(w1, gain1dB, w2, gain2dB, w3, gain3dB); %ゲイン線図をプロット
xlim([10^(-2),10^2]) %横軸（角周波数）の範囲の指定
ylim([-70 0]) %縦軸の範囲の指定
yticks([-60 -40 -20 0]) %縦軸の目盛りの値の設定
grid; %罫線を表示
xlabel('Frequency (rad/s)'); %横軸のラベル表示
ylabel('Gain [dB]'); %縦軸のラベル表示
legend('T=0.1', 'T=1', 'T=10'); %凡例の表示

%時間変数の定義
t = 0:0.01:60; %0から60まで0.01刻み

%ステップ応答の計算
[ y1 t1 ] = step( sys1, t ); %T=0.1の場合のステップ応答
[ y2 t2 ] = step( sys2, t ); %T=1の場合のステップ応答
[ y3 t3 ] = step( sys3, t ); %T=1.0の場合のステップ応答

%図12.14のステップ応答のプロット
subplot(2,1,2) %複数の図を並べるためのコマンド．2行1列の2行1列目という意味
plot(t1,y1,'-b',t2,y2,'-g',t3,y3,'-r'); %ステップ応答をプロット
xlim([0,60]) %横軸（時間軸）の範囲の指定
ylim([0 1.0]) %縦軸の範囲の指定
xticks([0 10 20 30 40 50 60]) %横軸の目盛りの値の設定
yticks([0 0.2 0.4 0.6 0.8 1.0]) %縦軸の目盛りの値の設定
grid; %罫線を表示
xlabel('time  t [s]'); %横軸のラベル表示
ylabel('output'); %縦軸のラベル表示
legend('T=0.1', 'T=1', 'T=10'); %凡例の表示