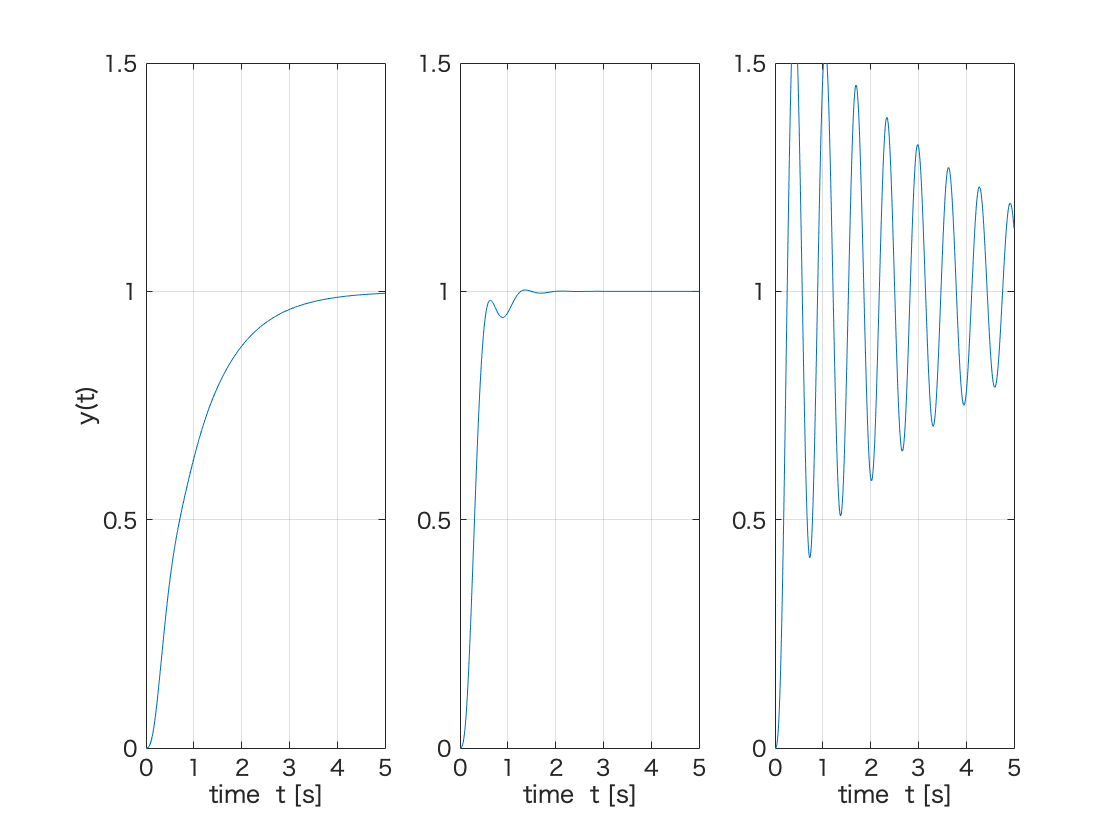
%図13.2 % clear all; close all; %図13.2のプロット %パラメータの値を与える K = 1; %K=1 omegan = 10; %ω_n=10 zeta = 0.5; %ζ=0.5 %伝達関数の分子・分母多項式を与える num = [ 0 0 K*omegan^2 ]; %ζ=0.5の場合の分子多項式 den = [ 1 2*zeta*omegan omegan^2 ]; %ζ=0.5の場合の分母多項式 %積分ゲインのパラメータを与える Ki1 = 1.0; %K_i=1 Ki2 = 3.0; %K_i=3 Ki3 = 9.0; %K_i=9 %コントローラの分子・分母多項式を与える. numc1 = [ 0 Ki1 ]; %K_i=1の場合の分子多項式 numc2 = [ 0 Ki2 ]; %K_i=3の場合の分子多項式 numc3 = [ 0 Ki3 ]; %K_i=9の場合の分子多項式 denc = [ 1 0 ]; %分母多項式 %制御対象とコントローラの伝達関数表現を与える sys = tf( num, den ); %制御対象の伝達関数表現 c1 = tf( numc1, denc ); %K_i=1.0の場合のコントローラの伝達関数表現 c2 = tf( numc2, denc ); %K_i=3の場合のコントローラの伝達関数表現 c3 = tf( numc3, denc ); %K_i=9の場合のコントローラの伝達関数表現 %コントローラと制御対象のフィードバック結合を求める sysc1 = feedback( c1*sys, 1 ); %K_i=1の場合のフィードバック結合 sysc2 = feedback( c2*sys, 1 ); %K_i=の3の場合のフィードバック結合 sysc3 = feedback( c3*sys, 1 ); %K_i=9の場合のフィードバック結合 %時間変数の定義 t = 0:0.01:5; %0から5まで0.01刻み %ステップ応答の計算 [ y1, t1 ] = step( sysc1, t ); %K_i=1の場合のステップ応答 [ y2, t2 ] = step( sysc2, t ); %K_i=3場合のステップ応答 [ y3, t3 ] = step( sysc3, t ); %K_i=9の場合のステップ応答 %図13.2(a)のプロット subplot(1,3,1) %複数の図を並べるためのコマンド.1行3列の1列目という意味 plot(t1,y1); %ステップ応答をプロット xlim([0,5]) %横軸(時間軸)の範囲の指定 ylim([0.0 1.5]) %縦軸の範囲の指定 xticks([0 1 2 3 4 5]) %横軸の目盛りの値の設定 yticks([0.0 0.5 1.0 1.5]) %縦軸の目盛りの値の設定 grid; %罫線を表示 xlabel('time t [s]'); %横軸のラベル表示 ylabel('y(t)') %縦軸のラベル表示 %図13.2(b)のプロット subplot(1,3,2) %複数の図を並べるためのコマンド.1行3列の2列目という意味 plot(t2,y2); %ステップ応答をプロット xlim([0,5]) %横軸(時間軸)の範囲の指定 ylim([0.0 1.5]) %縦軸の範囲の指定 xticks([0 1 2 3 4 5]) %横軸の目盛りの値の設定 yticks([0.0 0.5 1.0 1.5]) %縦軸の目盛りの値の設定 grid; %罫線を表示 xlabel('time t [s]'); %横軸のラベル表示 %ylabel('y(t)') %縦軸のラベル表示 %図13.2(c)のプロット subplot(1,3,3) %複数の図を並べるためのコマンド.1行3列の3列目という意味 plot(t3,y3); %ステップ応答をプロット xlim([0,5]) %横軸(時間軸)の範囲の指定 ylim([0.0 1.5]) %縦軸の範囲の指定 xticks([0 1 2 3 4 5]) %横軸の目盛りの値の設定 yticks([0.0 0.5 1.0 1.5]) %縦軸の目盛りの値の設定 grid; %罫線を表示 xlabel('time t [s]'); %横軸のラベル表示 %ylabel('y(t)') %縦軸のラベル表示