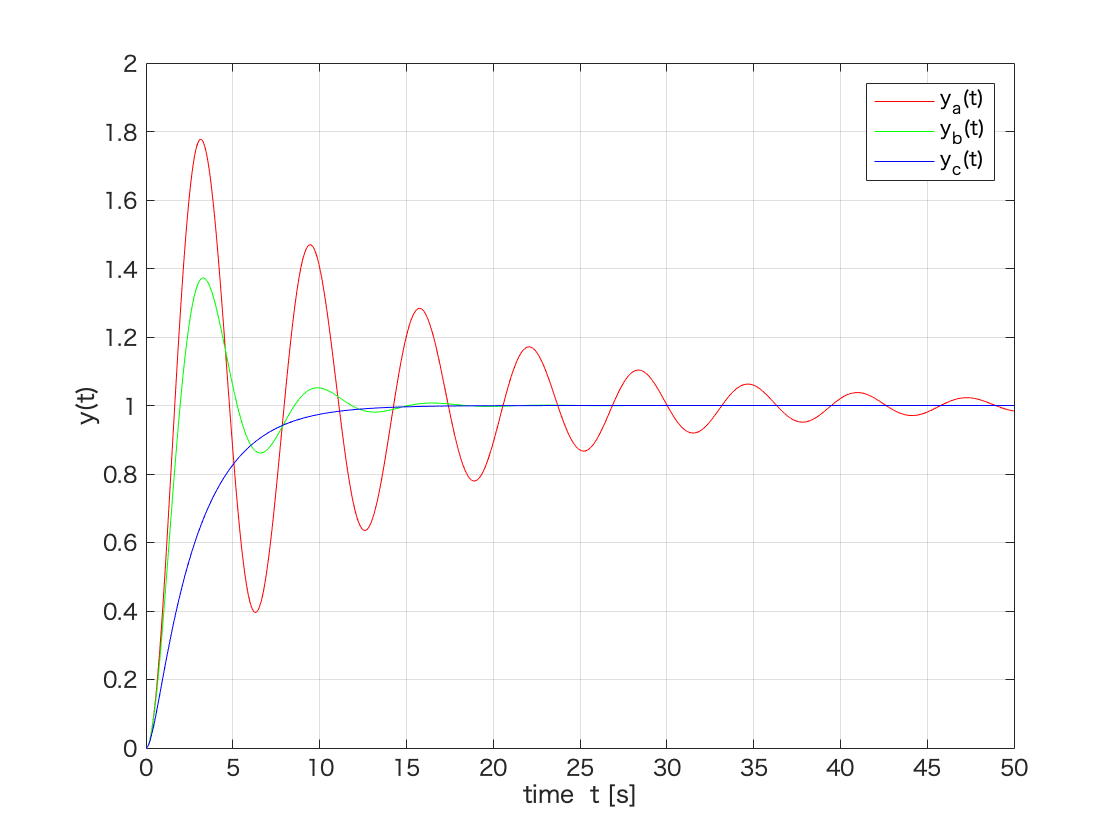
%図5.3 % clear all; close all; %伝達関数の分子・分母多項式を与える num = [ 0 0 1 ]; %分子多項式 den1 = [ 1 2*0.08*1 1 ]; %y_a(t)の分母多項式 den2 = [ 1 2*0.3*1 1 ]; %y_b(t)の分母多項式 den3 = [ 1 2*1.5*1 1 ]; %y_c(t)の分母多項式 %伝達関数表現を与える sys1 = tf( num,den1 ); %y_a(t)の伝達関数表現 sys2 = tf( num,den2 ); %y_b(t)の伝達関数表現 sys3 = tf( num,den3 ); %y_c(t)の伝達関数表現 %時間変数の定義 t = 0:0.01:50; %0から50まで0.01刻み %ステップ応答の計算 [ y1 t1 ] = step( sys1, t ); %y_a(t)のステップ応答 [ y2 t2 ] = step( sys2, t ); %y_b(t)のステップ応答 [ y3 t3 ] = step( sys3, t ); %y_c(t)のステップ応答 %図5.3のプロット plot(t1,y1,'-r',t2,y2,'-g',t3,y3,'-b'); %ステップ応答をプロット ylim([0,2]) %縦軸の範囲の指定 grid; %罫線を表示 xlabel('time t [s]'); %横軸のラベル表示 ylabel('y(t)'); %縦軸のラベル表示 legend('y_a(t)','y_b(t)','y_c(t)'); %凡例の表示