Fig_6_10

%図6.10
%
clear all; close all;

%パラメータの値を与える
K = 1; %K=1
omegan = 1; %ω_n=1
zeta1 = 1.1; %ζ=1.1
zeta2 = 1.5; %ζ=1.5
zeta3 = 2.0; %ζ=2.0

%伝達関数の分子・分母多項式を与える
num = [ 0 0 K*omegan^2 ]; %分子多項式
den1 = [ 1 2*zeta1*omegan omegan^2 ]; %ζ=1.1の場合の分母多項式
den2 = [ 1 2*zeta2*omegan omegan^2 ]; %ζ=1.5の場合の分母多項式
den3 = [ 1 2*zeta3*omegan omegan^2 ]; %ζ=2.0の場合の分母多項式

%伝達関数表現を与える
sys1 = tf( num, den1 ); %ζ=1.1の場合の伝達関数表現
sys2 = tf( num, den2 ); %ζ=1.5の場合の伝達関数表現
sys3 = tf( num, den3 ); %ζ=2.0の場合の伝達関数表現

%時間変数の定義
t = 0:0.01:20; %0から20まで0.01刻み

%ステップ応答の計算
[ y1, t1 ] = step( sys1, t ); %ζ=1.1の場合のステップ応答
[ y2, t2 ] = step( sys2, t ); %ζ=1.5の場合のステップ応答
[ y3, t3 ] = step( sys3, t ); %ζ=2.0の場合のステップ応答

%図6.10のプロット
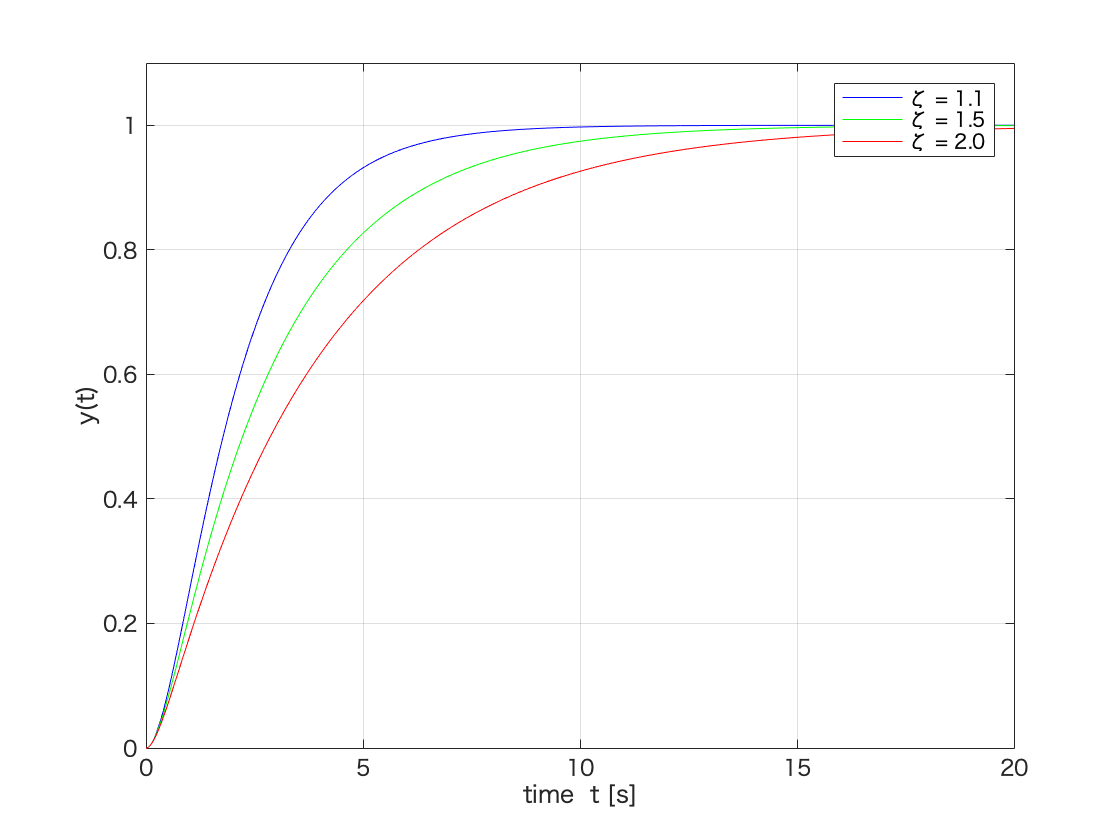
plot(t1,y1,'-b',t2,y2,'-g',t3,y3,'-r'); %ステップ応答をプロット
xlim([0,20]) %横軸（時間軸）の範囲の指定
ylim([0.0,1.1]) %縦軸の範囲の指定
xticks([0 5 10 15 20]) %横軸の目盛りの値の設定
yticks([0.0 0.2 0.4 0.6 0.8 1.0]) %縦軸の目盛りの値の設定
grid; %罫線を表示
xlabel('time  t [s]'); %横軸のラベル表示
ylabel('y(t)') %縦軸のラベル表示
legend('ζ = 1.1','ζ = 1.5','ζ = 2.0'); %凡例の表示