Fig_6_12_6

%図6.12, 図6.13
%
clear all; close all;

%パラメータの値を与える
A = 1; %A=1
phi = pi/6.0; %φ=π/6
omega1 = 2.0 * pi; %ω=2π
omega2 = 4.0 * pi; %ω=4π
omega3 = 8.0 * pi; %ω=8π

%時間変数の定義
t = 0:0.001:2; %0から2まで0.001刻み

%インパルス応答の計算
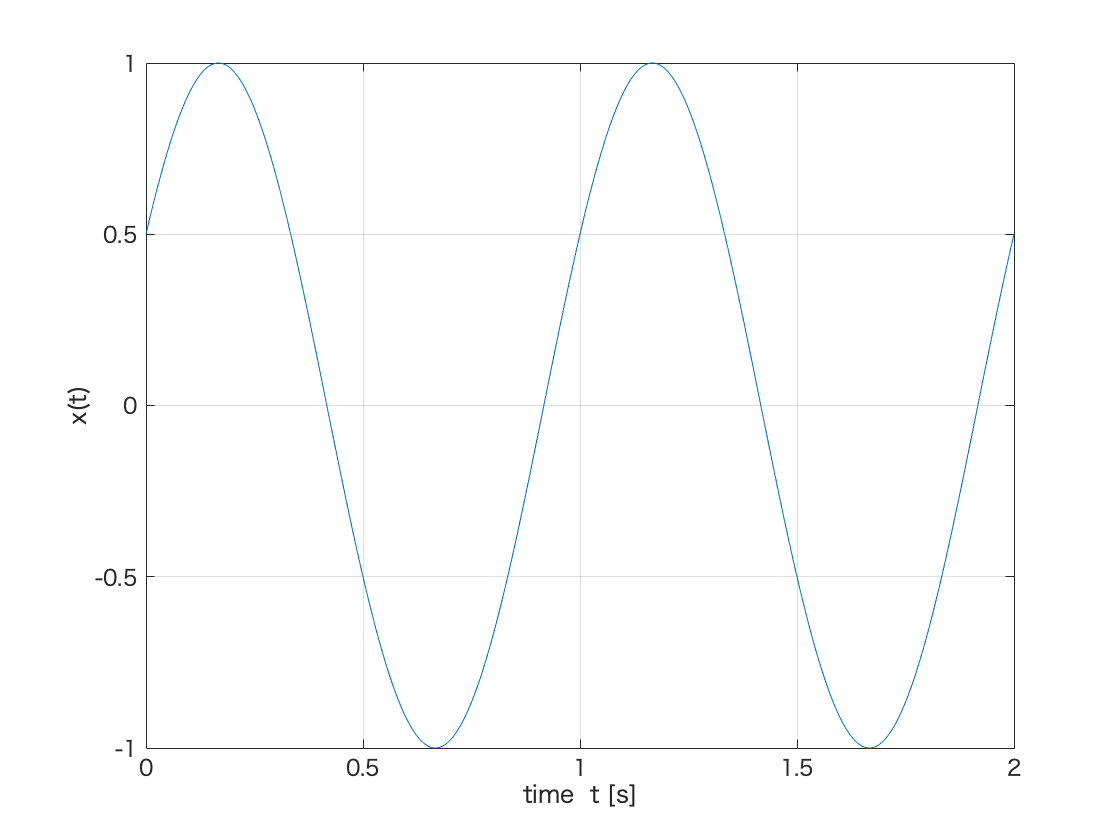
x0 = A * sin( omega1 * t + phi); %φ=π/6, ω=2πの場合の正弦波
x1 = A * sin( omega1 * t + phi); %φ=π/6, ω=2πの場合の正弦波
x2 = A * sin( omega2 * t + phi); %φ=π/6, ω=4πの場合の正弦波
x3 = A * sin( omega3 * t + phi); %φ=π/6, ω=8πの場合の正弦波

%図6.12のプロット
figure(1); %図のウィンドウを開く

plot(t,x0); %e^{at}の値をプロット
xlim([0,2.0]) %横軸（時間軸）の範囲の指定
xticks([0 0.5 1.0 1.5 2.0]) %横軸の目盛りの値の設定
yticks([-1.0 -0.5 0 0.5 1.0]) %縦軸の目盛りの値の設定
grid; %罫線を表示
xlabel('time  t [s]'); %横軸のラベル表示
ylabel('x(t)'); %縦軸のラベル表示

%図6.13のプロット
figure(2); %図のウィンドウを開く

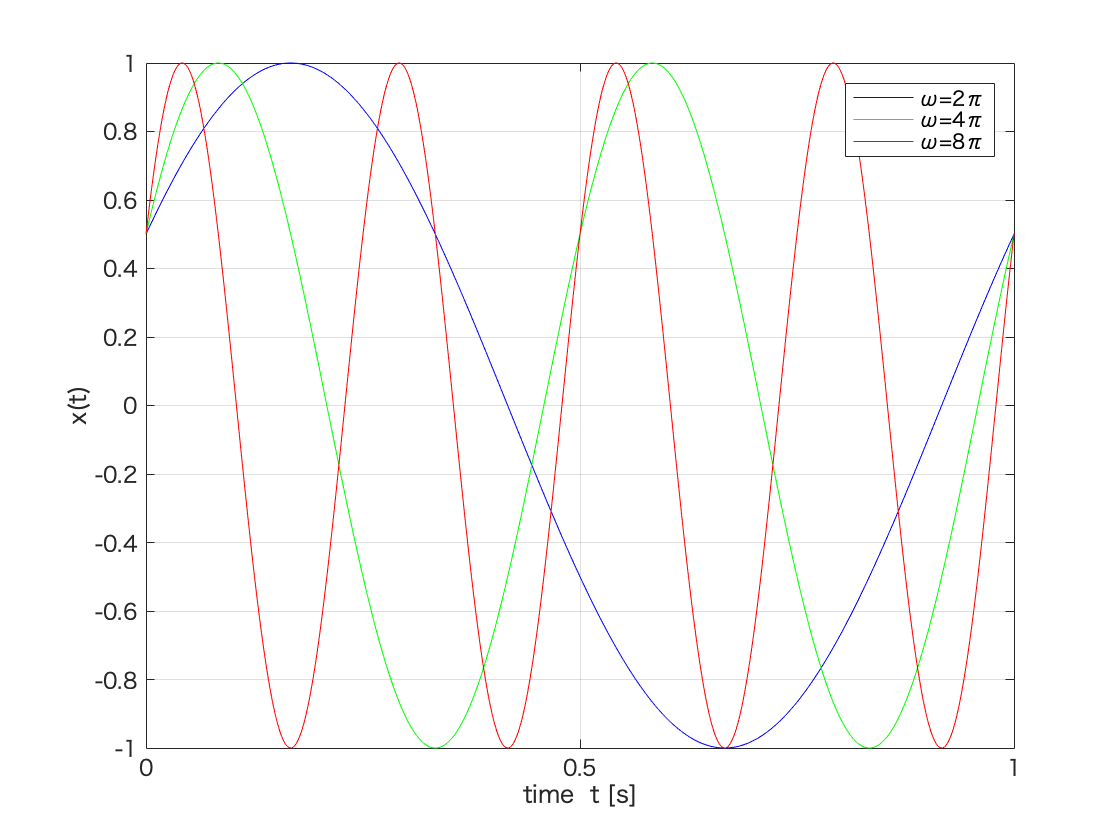
plot(t,x1,'-b',t,x2,'-g',t,x3,'-r'); %ωの値に応じたx(t)をプロット
xlim([0,1.0]) %横軸（時間軸）の範囲の指定
xticks([0 0.5 1.0 1.5 2.0]) %横軸の目盛りの値の設定
yticks([-1.0 -0.8 -0.6 -0.4 -0.2 0 0.2 0.4 0.6 0.8 1.0]) %縦軸の目盛りの値の設定
grid; %罫線を表示
xlabel('time  t [s]'); %横軸のラベル表示
ylabel('x(t)'); %縦軸のラベル表示
legend('ω=2π','ω=4π','ω=8π'); %凡例の表示