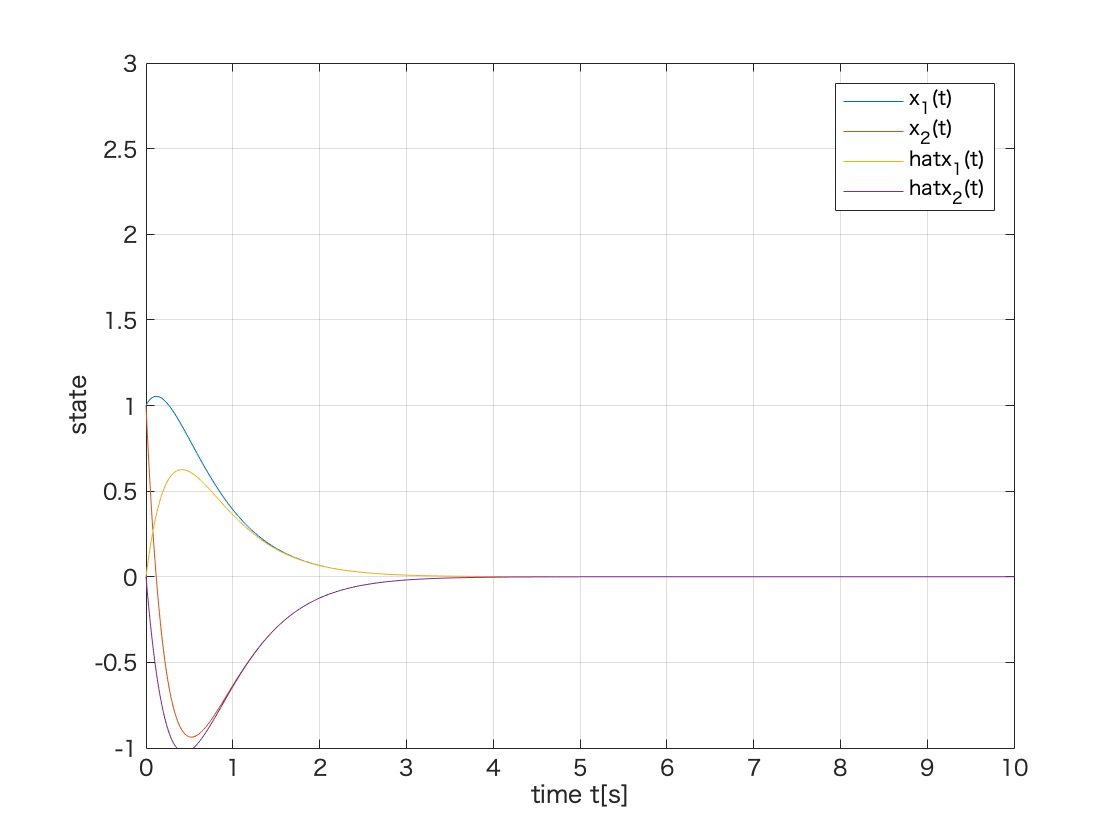
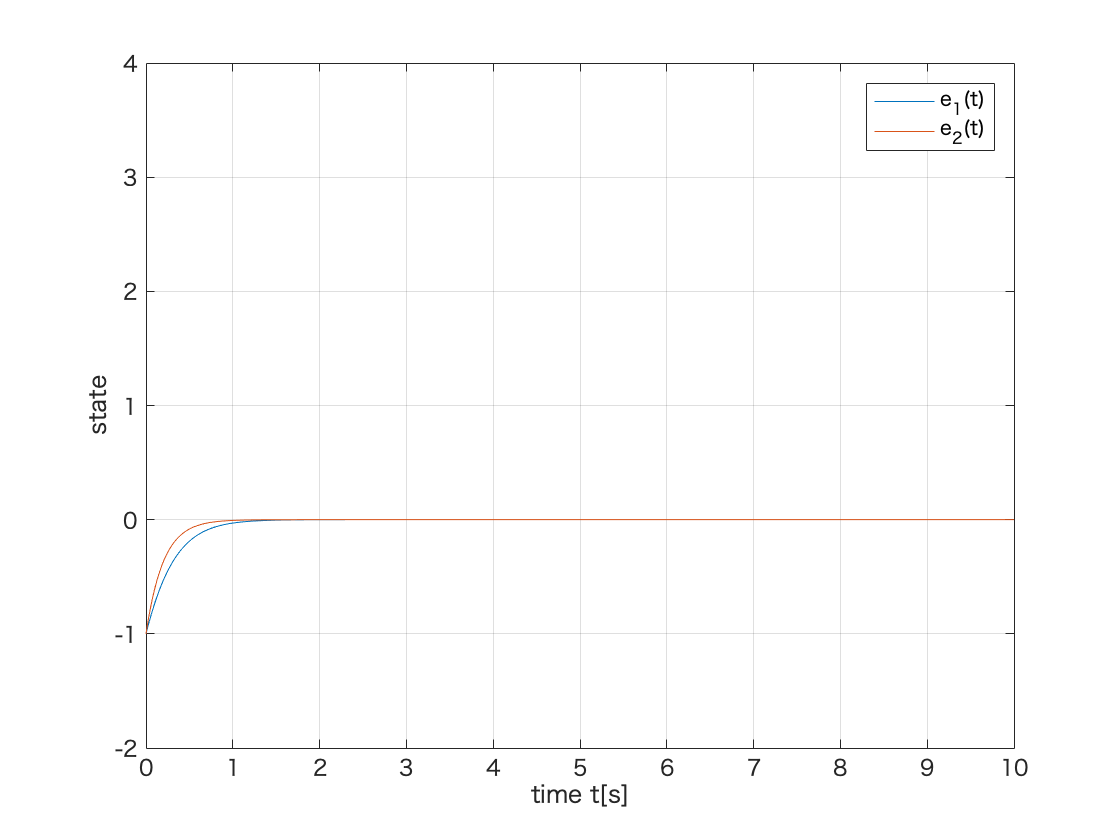
%図11.4 clear all; close all; %システムパラメータを与える A = [0 1;-6 -5]; %行列A b = [0;1]; %ベクトルb c = [1 0]; %ベクトルc d = 0; %スカラーd %配置するオブザーバの極を与える op = [-4;-5]; %-4, -5をオブザーバの極とする %オブザーバゲインを求める.双対システムA^Tとc^Tの状態フィードバックゲインを求め,転置を取るとオブザーバゲインとなる h = acker(A',c',op)' %双対システムで極配置し,転置を求める %Ah = A-hcとオブザーバの極の計算と表示 Ah = A - h*c; %Ah = A - h*cの計算 disp('A-hcの固有値'); eig(A - h * c) %オブザーバの極を計算し表示 %システムとオブザーバ(誤差システム(11.15)式)の状態空間表現を求める cc = eye(2); %オブザーバの状態変数をプロットするためにCを単位行列にする dd = [0;0]; %cに合わせてDは零ベクトルとする sys = ss(A, b, cc, dd); %システムの状態空間表現 e_sys = ss(Ah, b, cc, dd); %誤差システムの状態空間表現 %時間変数の定義 t = 0:0.01:10; %0から10まで0.01刻み %システムとオブザーバの初期値を与える x0 = [1;1]; %システムの初期値 x0_ob = [0;0]; %オブザーバの初期値 %初期値応答の計算 y = initial(sys,x0,t); %f1の場合の初期値応答 e = initial(e_sys,x0_ob - x0,t); %f2の場合の初期値応答 %オブザーバの状態を求める h_x = e + y; %e(t) = hat{x}(t) - x(t)よりhat{x}を求める %図11.4(a)のプロット figure(1) %図のウィンドウを開く plot(t,y(:,1),t,y(:,2),t,h_x(:,1),t,h_x(:,2)); %各状態を抽出してプロット xlim([0 10]); %横軸(時間軸)の範囲の指定 ylim([-1.0 3.0]); %縦軸の範囲の設定 grid; %罫線を表示 xlabel('time t[s]'); %横軸のラベル表示 ylabel('state'); %縦軸のラベル表示 legend('x_1(t)','x_2(t)','hat{x}_1(t)','hat{x}_2(t)'); %凡例の表示 %図11.4(b)のプロット figure(2) %図のウィンドウを開く plot(t,e(:,1),t,e(:,2)); %各状態を抽出してプロット xlim([0 10]); %横軸(時間軸)の範囲の指定 ylim([-2.0 4.0]); %縦軸の範囲の設定 grid; %罫線を表示 xlabel('time t[s]'); %横軸のラベル表示 ylabel('state'); %縦軸のラベル表示 legend('e_1(t)','e_2(t)'); %凡例の表示
h =
4
-6
A-hcの固有値
ans =
-4
-5