Fig_13_5_13

%図13.5, 13.6

clear all; close all;

%システムパラメータを与える
A = [0 1;-6 -5]; %行列A
b = [0;1]; %ベクトルb
c = [1 0]; %ベクトルc
d = 0; %スカラーd

%状態フィードバックによる閉ループの極
fbp = [-3; -3];

%フィードバックゲインを求める
disp('求めるフィードバックゲイン');
f =  acker(A,b,fbp)
Af = A - b * f
disp('閉ループ極')
eig(A - b * f)

%システムの状態空間表現を求める
cp = eye(2); %オブザーバの状態変数をプロットするためにCを単位行列にする
dp = [0;0]; %cに合わせてDは零ベクトルとする

sys_s_fbk = ss(Af, b, cp, dp); %システムの状態空間表現

%時間変数の定義
t = 0:0.01:5; %0から5まで0.01刻み

%システムの初期値を与える
x0 = [-1;0]; %システムの初期値

%初期値応答の計算
y = initial(sys_s_fbk,x0,t); %状態フィードバック系の初期値応答

%図13.5のプロット
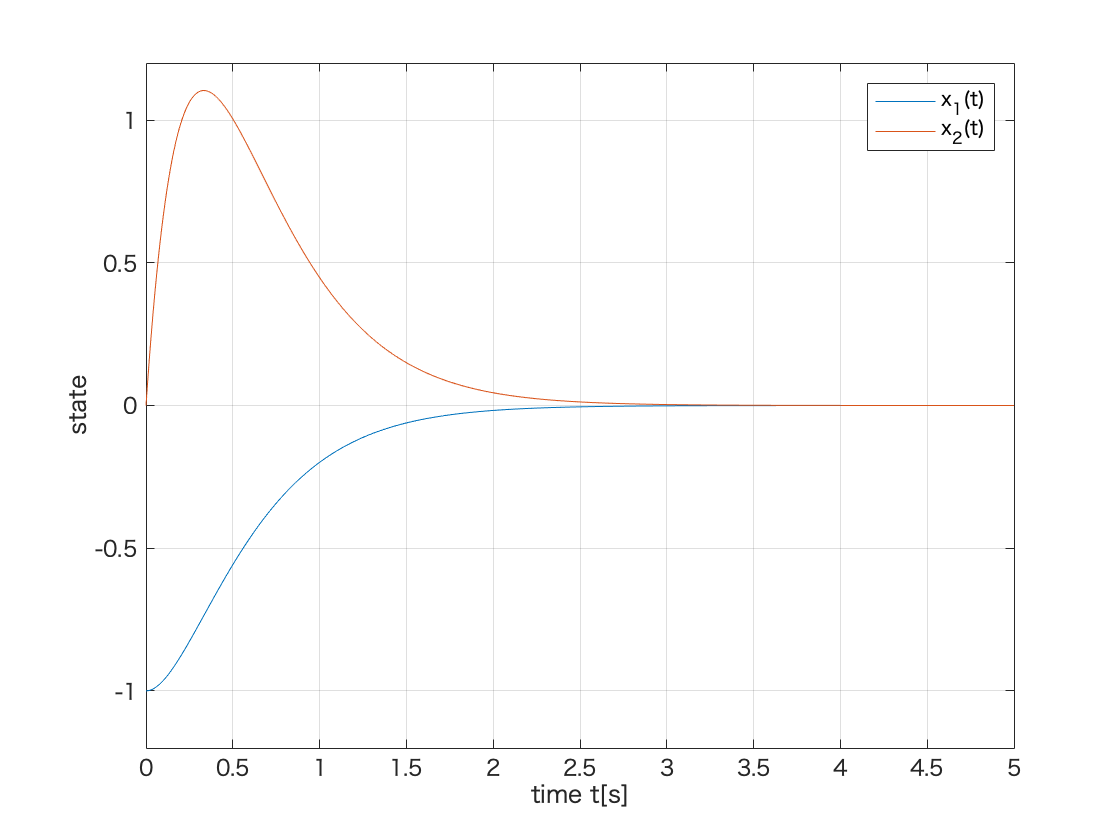
figure(1) %図のウィンドウを開く
plot(t,y(:,1),t,y(:,2)); %各状態を抽出してプロット
xlim([0 5]); %横軸（時間軸）の範囲の指定
ylim([-1.2 1.2]); %縦軸の範囲の設定
grid; %罫線を表示
xlabel('time t[s]'); %横軸のラベル表示
ylabel('state'); %縦軸のラベル表示
legend('x_1(t)','x_2(t)'); %凡例の表示

dd = ones([1,length(t)]); %単位ステップ信号で表される外乱

%初期値応答の計算
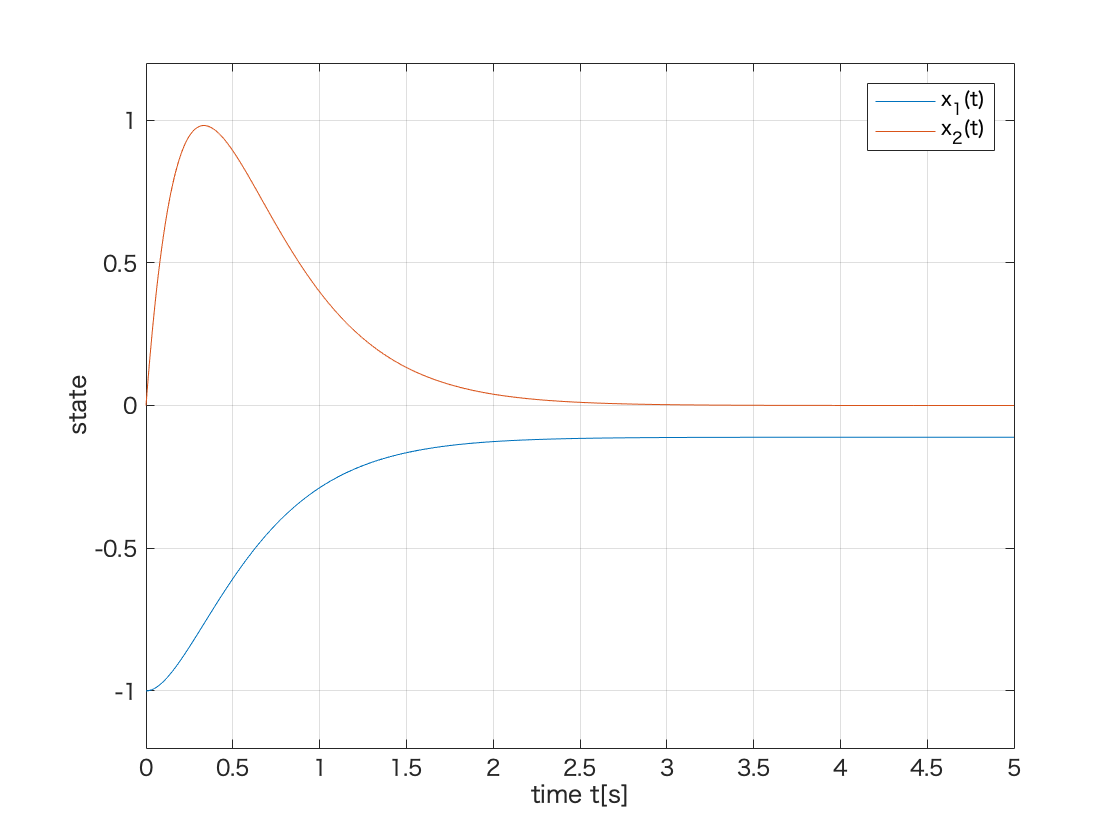
yd = lsim(sys_s_fbk,-dd,t,x0); %状態フィードバック系の初期値応答

%図13.6のプロット
figure(2) %図のウィンドウを開く
plot(t,yd(:,1),t,yd(:,2)); %各状態を抽出してプロット
xlim([0 5]); %横軸（時間軸）の範囲の指定
ylim([-1.2 1.2]); %縦軸の範囲の設定
grid; %罫線を表示
xlabel('time t[s]'); %横軸のラベル表示
ylabel('state'); %縦軸のラベル表示
legend('x_1(t)','x_2(t)'); %凡例の表示

求めるフィードバックゲイン

f =

     3     1


Af =

     0     1
    -9    -6

閉ループ極

ans =

  -3.0000 + 0.0000i
  -3.0000 - 0.0000i