Fig_9_1_9

%図9.1, 9.2
clear all; close all;

%システムパラメータを与える
A = [0 1;-2 -3]; %行列A
b = [0;1]; %ベクトルb
c = [1 0;0 1]; %x_1とx_2をプロットするためにcを単位行列にする
d = [0;0]; %cに合わせてdは零ベクトルとする

%システム行列Aの固有値を求める
eig(A) %システム行列Aの固有値

%配置する極を与える
p1 = [-2; -3]; %-2, -3の場合
p2 = [-5; -6]; %-5, -6の場合

%アッカーマンの方法によりフィードバックゲインを求める
disp('求めるフィードバックゲイン');
f1 =  acker(A,b,p1) %-2, -3の場合のフィードバックゲインf1
f2 =  acker(A,b,p2) %-5, -6の場合のフィードバックゲインf2

%閉ループ極の表示
eig(A - b * f1) %f1の場合の閉ループ極
eig(A - b * f2) %f2の場合の閉ループ極

%閉ループシステムの状態空間表現を求める
sysC1 = ss(A-b*f1,b,c,d); %f1の場合の閉ループシステム
sysC2 = ss(A-b*f2,b,c,d); %f2の場合の閉ループシステム

%時間変数の定義
t = 0:0.01:10; %0から10まで0.01刻み

%システムの初期値を与える
x0 = [1 1]';

%初期値応答の計算
y1 = initial(sysC1,x0,t); %f1の場合の初期値応答
y2 = initial(sysC2,x0,t); %f2の場合の初期値応答

%図9.1のプロット
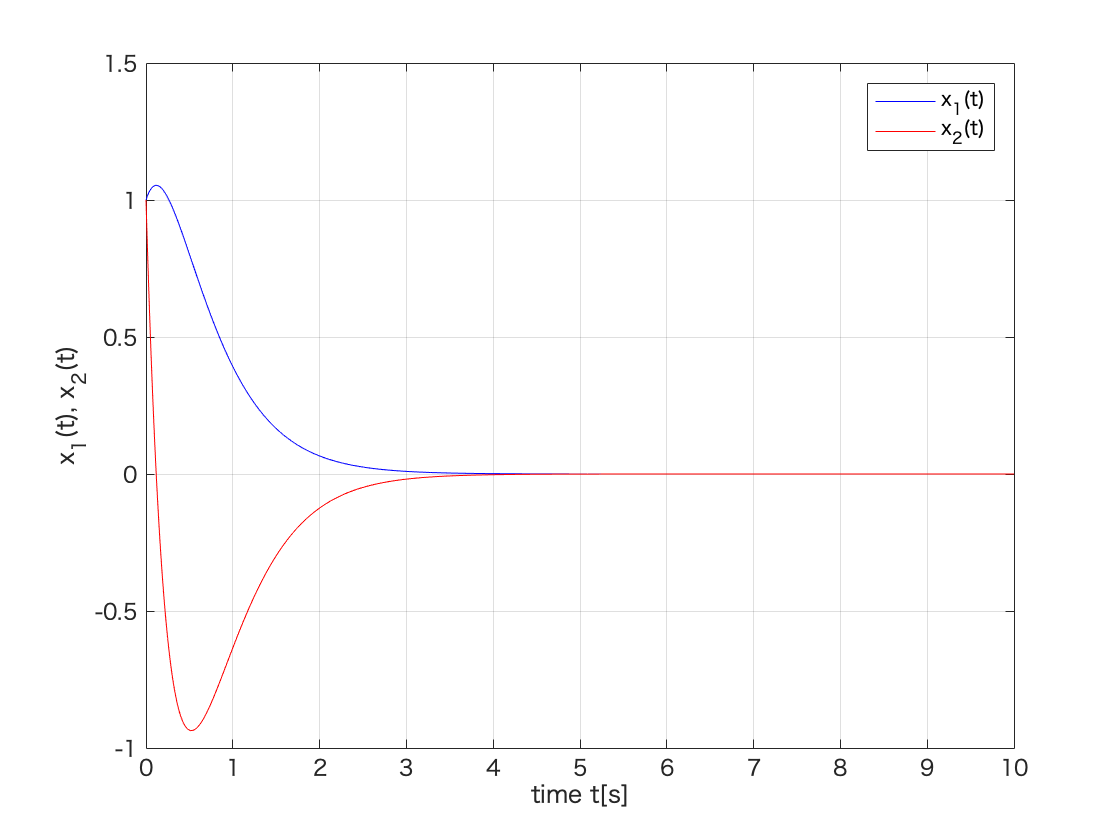
figure(1) %図のウィンドウを開く
plot(t,y1(:,1),'-b',t,y1(:,2),'-r'); %x_1とx_2を抽出してプロット
xlim([0 10]); %横軸（時間軸）の範囲の指定
ylim([-1.0 1.5]); %縦軸の範囲の設定
grid; %罫線を表示
xlabel('time t[s]'); %横軸のラベル表示
ylabel('x_1(t), x_2(t)'); %縦軸のラベル表示
legend('x_1(t)','x_2(t)'); %凡例の表示

%図9.2のプロット
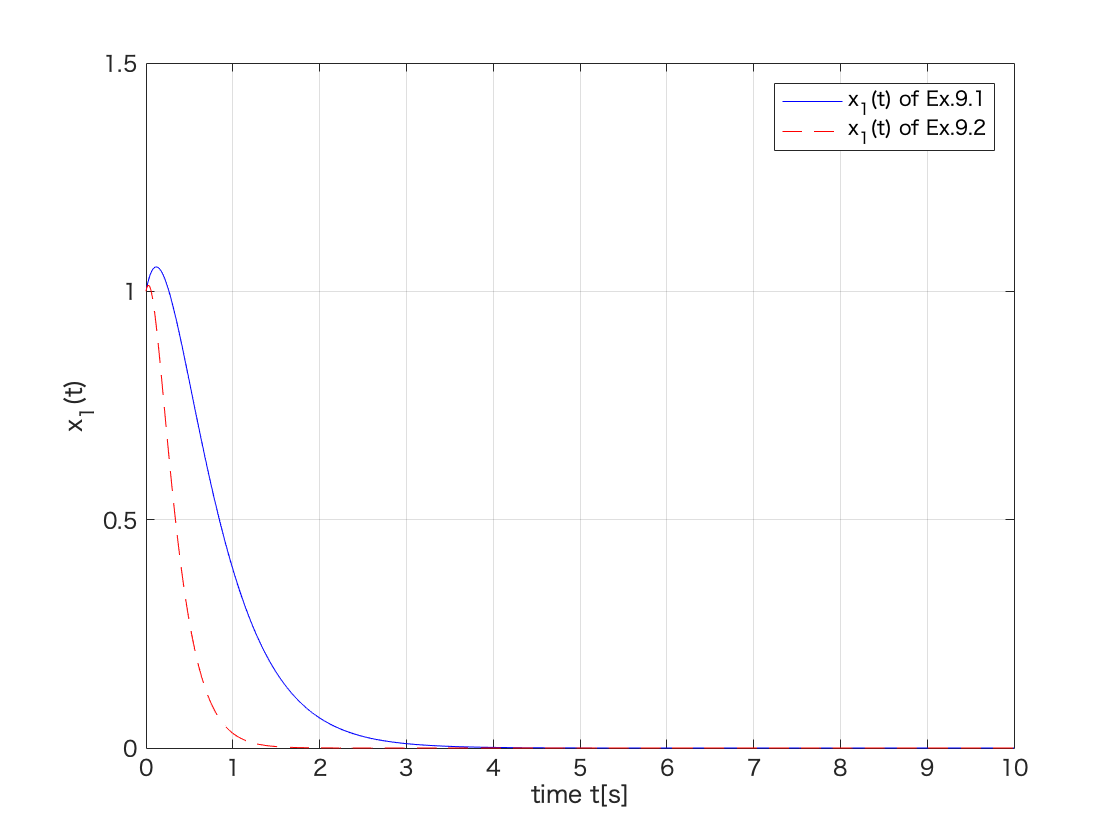
figure(2) %図のウィンドウを開く
plot(t,y1(:,1),'-b',t,y2(:,1),'--r');
xlim([0 10]); %横軸（時間軸）の範囲の指定
ylim([0.0 1.5]); %縦軸の範囲の設定
grid; %罫線を表示
xlabel('time t[s]'); %横軸のラベル表示
ylabel('x_1(t)'); %縦軸のラベル表示
legend('x_1(t) of Ex.9.1','x_1(t) of Ex.9.2'); %凡例の表示

%図9.2のプロット
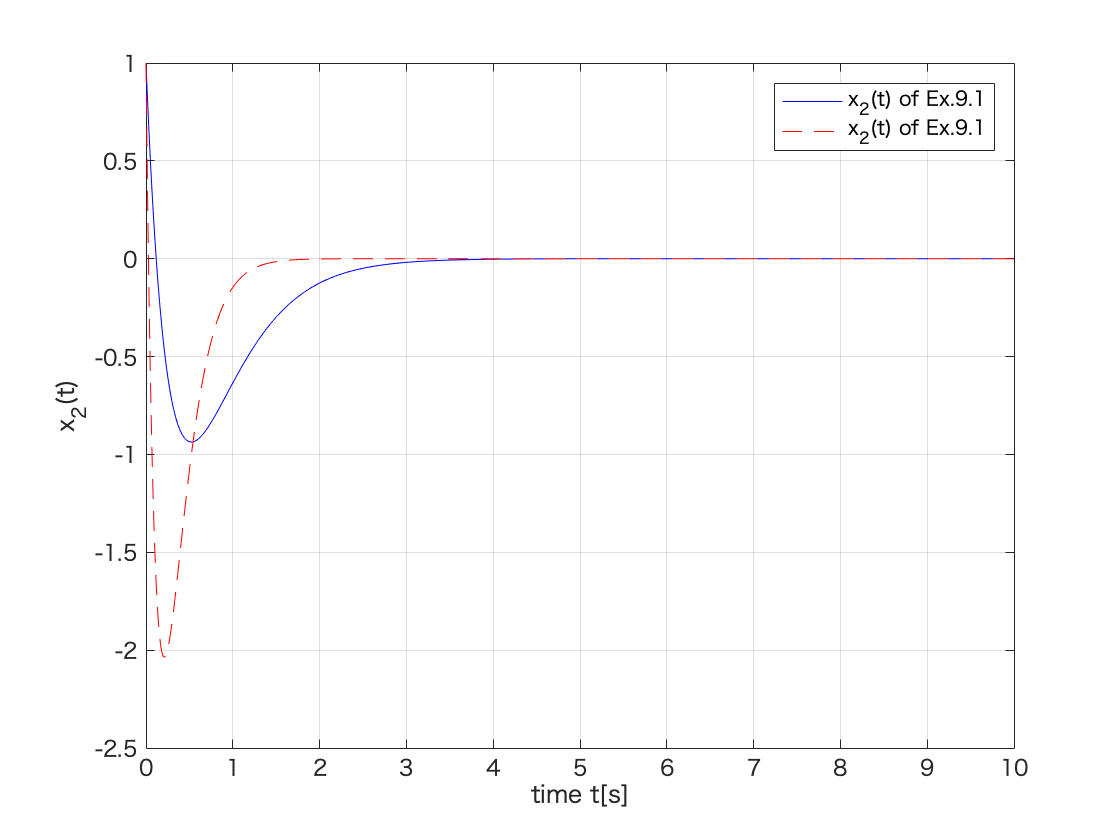
figure(3) %図のウィンドウを開く
plot(t,y1(:,2),'-b',t,y2(:,2),'--r');
xlim([0 10]); %横軸（時間軸）の範囲の指定
ylim([-2.5 1.0]); %縦軸の範囲の設定
grid; %罫線を表示
xlabel('time t[s]'); %横軸のラベル表示
ylabel('x_2(t)'); %縦軸のラベル表示
legend('x_2(t) of Ex.9.1','x_2(t) of Ex.9.1'); %凡例の表示

ans =

    -1
    -2

求めるフィードバックゲイン

f1 =

     4     2


f2 =

    28     8


ans =

   -2.0000
   -3.0000


ans =

   -5.0000
   -6.0000